1. Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. For math, science, nutrition, history.
2. 5/4 x 6 x 8' Red Cedar Decking. Please Note: Prices, promotions, styles and availability may vary by store and online. Inventory is sold and received continuously throughout the day; therefore, the quantity shown may not be available when you get to the store.
3. Download ExpanDrive for macOS or Windows for free. By downloading, installing and/or using ExpanDrive you agree to be bound by our End User License Agreement.

1. Expandrive 6 4 5 X 6 5
2. 4/5 As A Decimal
3. Expandrive 6 4 5 X 6
4. .net Framework 4.5

Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step-by-step explanations, just like a math tutor.

ExpanDrive 5 Crack + License Key Patch full. free download

ExpanDrive 5 Crack Full is a powerful network drive and auto cloud management tool that provides more cloud storage supports and super-fast file transfers. It allows user to access their cloud storage whatever the providers. ExpanDrive support for Google Drive, Dropbox, OneDrive, Amazon Cloud Drive, SFTP, Box, WebDAV, S3 and many more. ExpanDrive 5 acts just like detachable disk, you will be easily to access, open, edit, remove and transfer files from any apps between your desktop and the cloud service, not just as a conventional network drive.

ExpanDrive 5 License Key provides a multi-threaded connection engine that makes ExpanDrive faster and responsive than another sync apps. It permits you keep working on your projects because ExpanDrive working in the background and stop waiting for transfers to complete. ExpanDrive 5 delivers more cloud storage provider options than previews version, firmly access any remote file server directly from any explorer or terminal, manage remote files as if they were stored locally even all applications can access data.

ExpanDrive 5 Key Features:

• Quickly uploads your files in the background.
• Cloud storage in every application.
• Super-fast prompt uploads.
• ExpanDrive 5 Serial Key has inspiring complete control files management.
• Finder and Explorer is your user interface.
• It access distant files within any application.
• Provides friendly user interface.
• Permits you to manage files stored in Dropbox, OneDrive and so on.
• ExpanDrive 5 Patch transfer data to/or from your cloud account.
• Simple interface and tremendously easy to utilize.
• Simply connect to your cloud account.
• It can supports every Cloud.

What’s new in ExpanDrive 5 Keygen?

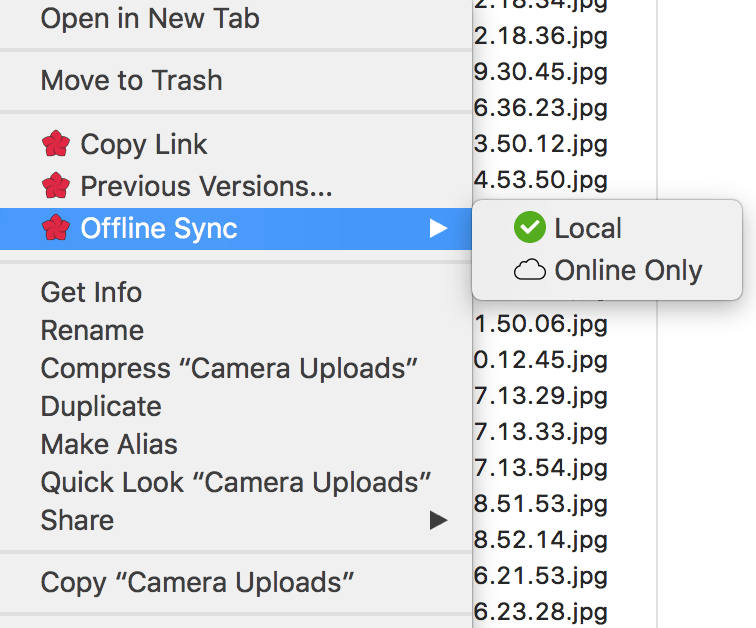
• Amazon Cloud Drive support
• Optimized for Windows 10
• New and other improvements
• Faster and more responsive
• Fusion online-offline mode

How to install ExpanDrive 5 Crack?

• Frist of all download ExpanDrive 5 Crack from given download link bellow.
• Then disconnect from internet.
• Follow the instructions and Install ExpanDrive 5 crack.
• Copy dll file from “Crack” to insdir#
• Or put the patch to insdir# and apply patch.
• #eg dir: “C:UsersMASTERkreatifAppDataLocalAppsExpanDrive“
• You have successfully completed installation procedure.
• All Done! Now enjoy this wonderful software.

Operating System:

Expandrive 6 4 5 X 6 5

• Windows XP
• Windows Vista
• Windows 7
• Windows 8
• Windows 8.1
• Windows 10

Screenshots:

ExpanDrive 5 Crack + License Key Patch Full Version Free Download from the link given below:

Purplemath

First you learned (back in grammar school) that you can add, subtract, multiply, and divide numbers. Then you learned that you can add, subtract, multiply, and divide polynomials. Now you will learn that you can also add, subtract, multiply, and divide functions. Performing these operations on functions is no more complicated than the notation itself. For instance, when they give you the formulas for two functions and tell you to find the sum, all they're telling you to do is add the two formulas. There's nothing more to this topic than that, other than perhaps some simplification of the expressions involved.

MathHelp.com

• Given f (x) = 3x + 2 and g(x) = 4 – 5x, find (f + g)(x), (f – g)(x), (f × g)(x), and (f / g)(x).

To find the answers, all I have to do is apply the operations (plus, minus, times, and divide) that they tell me to, in the order that they tell me to.

(f + g)(x) = f (x) + g(x)

= [3x + 2] + [4 – 5x]

= 3x + 2 + 4 – 5x

= 3x – 5x + 2 + 4

= –2x + 6

(f – g)(x) = f (x) – g(x)

= [3x + 2] – [4 – 5x]

= 3x + 2 – 4 + 5x

= 3x + 5x + 2 – 4

= 8x – 2

(f × g)(x) = [f (x)][g(x)]

= (3x + 2)(4 – 5x)

= 12x + 8 – 15x² – 10x

= –15x² + 2x + 8

My answer is the neat listing of each of my results, clearly labelled as to which is which.

( f + g ) (x) = –2x + 6

4/5 As A Decimal

( f – g ) (x) = 8x – 2

( f × g ) (x) = –15x² + 2x + 8

(f /g)(x) = (3x + 2)/(4 – 5x)

Content Continues Below

• Given f (x) = 2x, g(x) = x + 4, and h(x) = 5 – x³, find (f + g)(2), (h – g)(2), (f × h)(2), and (h / g)(2).

This exercise differs from the previous one in that I not only have to do the operations with the functions, but I also have to evaluate at a particular x-value. To find the answers, I can either work symbolically (like in the previous example) and then evaluate, or else I can find the values of the functions at x = 2 and then work from there. It's probably simpler in this case to evaluate first, so:

f (2) = 2(2) = 4

g(2) = (2) + 4 = 6

h(2) = 5 – (2)³ = 5 – 8 = –3

Now I can evaluate the listed expressions:

(f + g)(2) = f (2) + g(2)

(h – g)(2) = h(2) – g(2)

= –3 – 6 = –9

(f × h)(2) = f (2) × h(2)

(h / g)(2) = h(2) ÷ g(2)

= –3 ÷ 6 = –0.5

Then my answer is:

(f + g)(2) = 10, (h – g)(2) = –9, (f × h)(2) = –12, (h / g)(2) = –0.5

If you work symbolically first, and plug in the x-value only at the end, you'll still get the same results. Either way will work. Evaluating first is usually easier, but the choice is up to you.

You can use the Mathway widget below to practice operations on functions. Try the entered exercise, or type in your own exercise. Then click the button and select 'Solve' to compare your answer to Mathway's. (Or skip the widget and continue with the lesson.)

Please accept 'preferences' cookies in order to enable this widget.

(Clicking on 'Tap to view steps' on the widget's answer screen will take you to the Mathway site for a paid upgrade.)

• Givenf (x) = 3x² – x + 4, find the simplified form of the following expression, and evaluate at h = 0:

This isn't really a functions-operations question, but something like this often arises in the functions-operations context. This looks much worse than it is, as long as I'm willing to take the time and be careful.

Affiliate

The simplest way for me to proceed with this exercise is to work in pieces, simplifying as I go; then I'll put everything together and simplify at the end.

For the first part of the numerator, I need to plug the expression 'x + h' in for every 'x' in the formula for the function, using what I've learned about function notation, and then simplify:

f(x + h)

= 3(x + h)² – (x + h) + 4

= 3(x² + 2xh + h²) – x – h + 4

= 3x² + 6xh + 3h² – x – h + 4

The expression for the second part of the numerator is just the function itself:

Now I'll subtract and simplify:

f(x + h) – f(x)

= [3x² + 6xh + 3h² – x – h + 4] – [3x² – x + 4]

= 3x² + 6xh + 3h² – x – h + 4 – 3x² + x – 4

= 3x² – 3x² + 6xh + 3h² – x + x – h + 4 – 4

= 6xh + 3h² – h

All that remains is to divide by the denominator; factoring lets me simplify:

Now I'm supposed to evaluate at h = 0, so:

6x + 3(0) – 1 = 6x – 1

simplified form: 6x + 3h – 1

Expandrive 6 4 5 X 6

value at h = 0: 6x – 1

Affiliate

That's pretty much all there is to 'operations on functions' until you get to function composition. Don't let the notation for this topic worry you; it means nothing more than exactly what it says: add, subtract, multiply, or divide; then simplify and evaluate as necessary. Don't overthink this. It really is this simple.

Oh, and that last example? They put that in there so you can 'practice' stuff you'll be doing in calculus. You likely won't remember this by the time you actually get to calculus, but you'll follow a very similar process for finding something called 'derivatives'.

.net Framework 4.5

URL: https://www.purplemath.com/modules/fcnops.htm